Handling of subgeometries

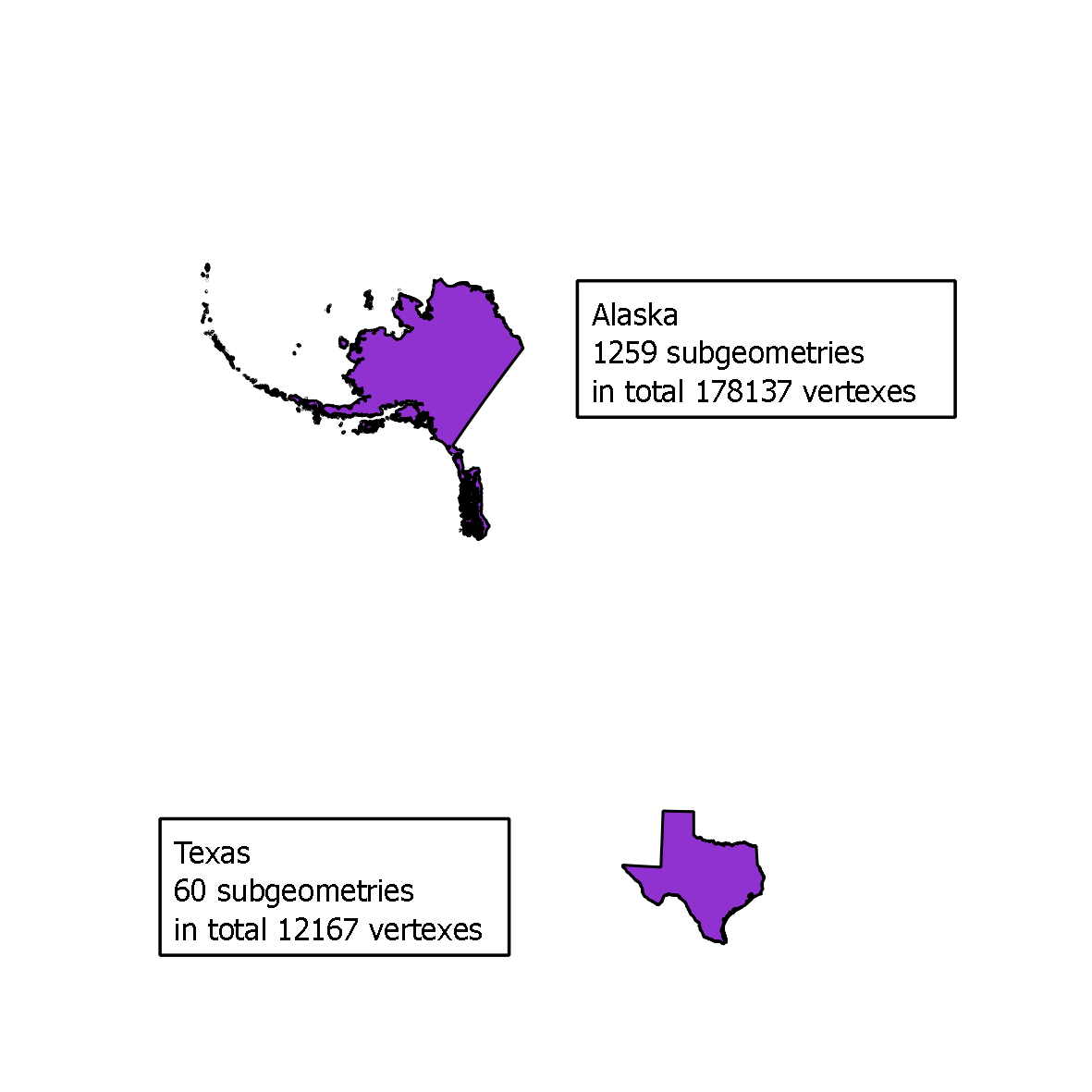
Calculating distances is quite a costly process. Because of that it is often worth the effort to sort the geometries depending on how the bounding boxes are related to each other. This example is a little extreme in the amount of subgeometries and vertexes but then the gain will really show. The example is a distance-calculation between Texas and Alaska.

In postgis 1.4 this would cause 178137 * 12167 = 2 167 392 879 iterations. This uses about 1440 seconds (22 minutes and 20 seconds). With the faster algorithm described in How the distance calculations is done the iterations will be very much reduced and then takes about 7 seconds. But even now there is a lot of unnecessary work done when calculating the exact distance to each and every of the sub geometries. This is how we now instead uses bounding boxes to only calculate a selection of geometries.

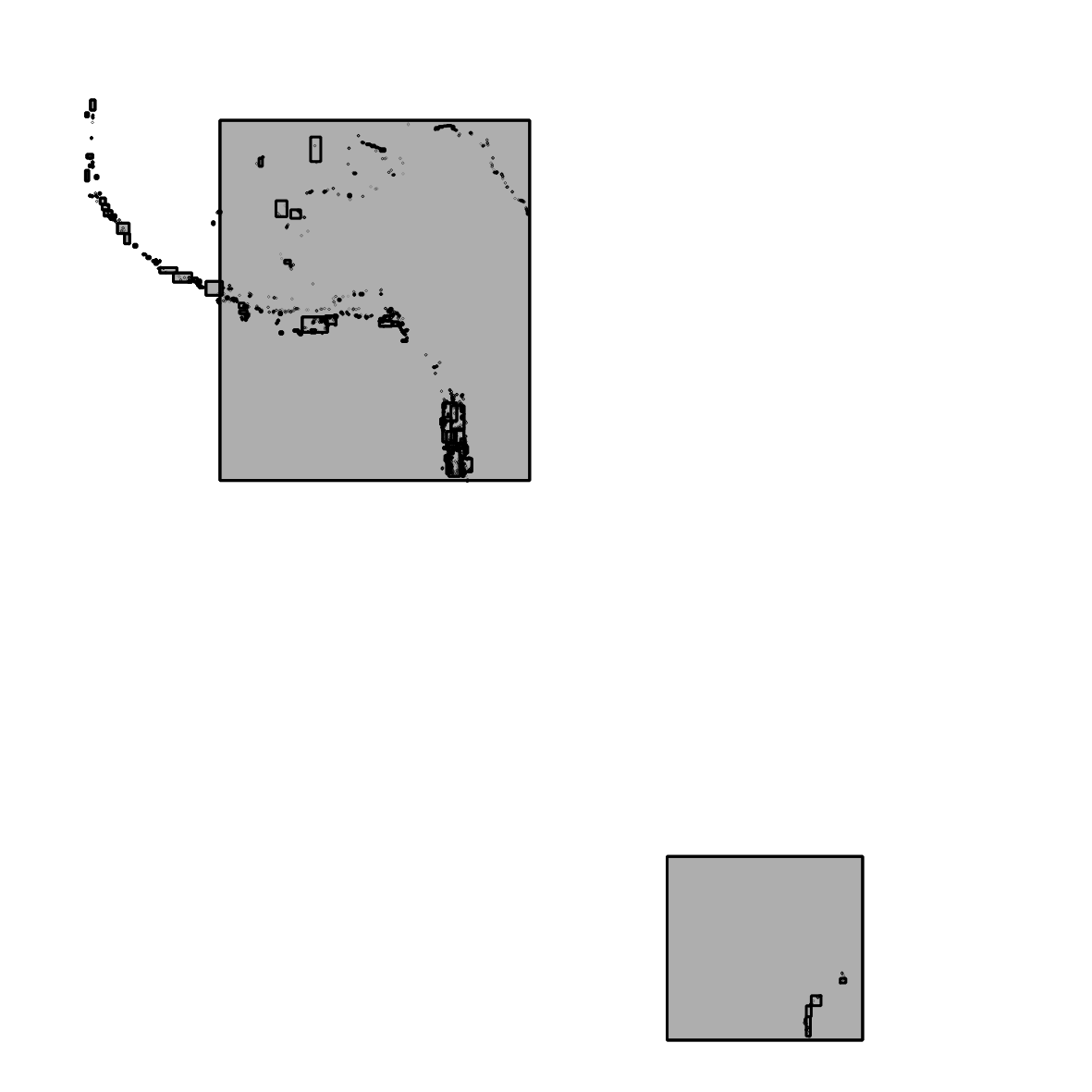
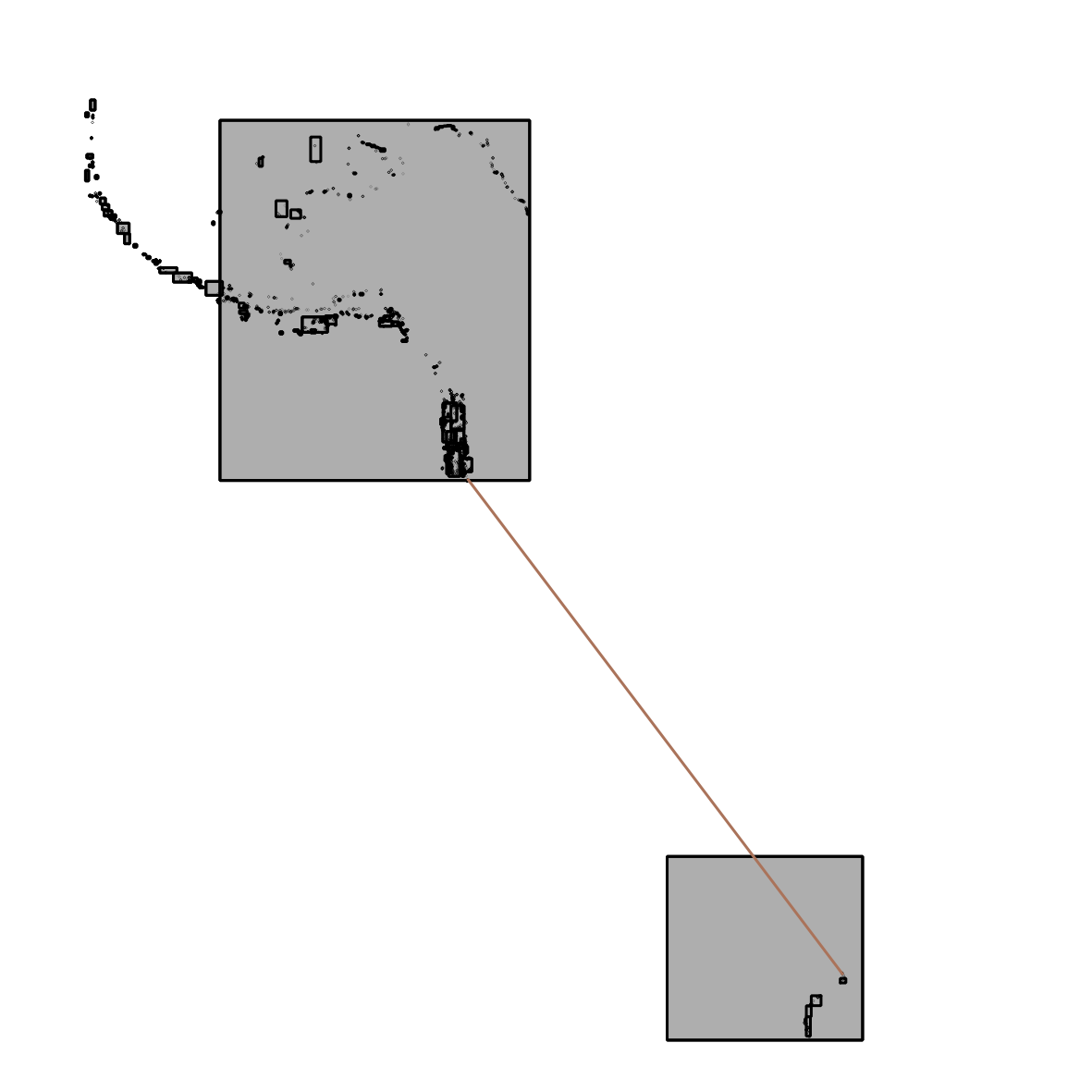
Here is the bounding boxes of the two states. Because postgis can handle nested geometrycollections, the first thing we have to du is "unwind" the collection or multi geometries so we get them in a "flat list" with all sub geometries without hierarchical order. Then we iterate through all combinations of bounding boxes to find the “smallest max distance” between the boxes. What we know from this value is that the distance we get here is longer or the same (if two inputed points) than the min distance we are looking for. The result is the distance along a line like this:

Now we iterate through all the combinations again and store all combinations with smaller min distance than the earlier found in a list. We also order the list so we get the smallest min distance first.

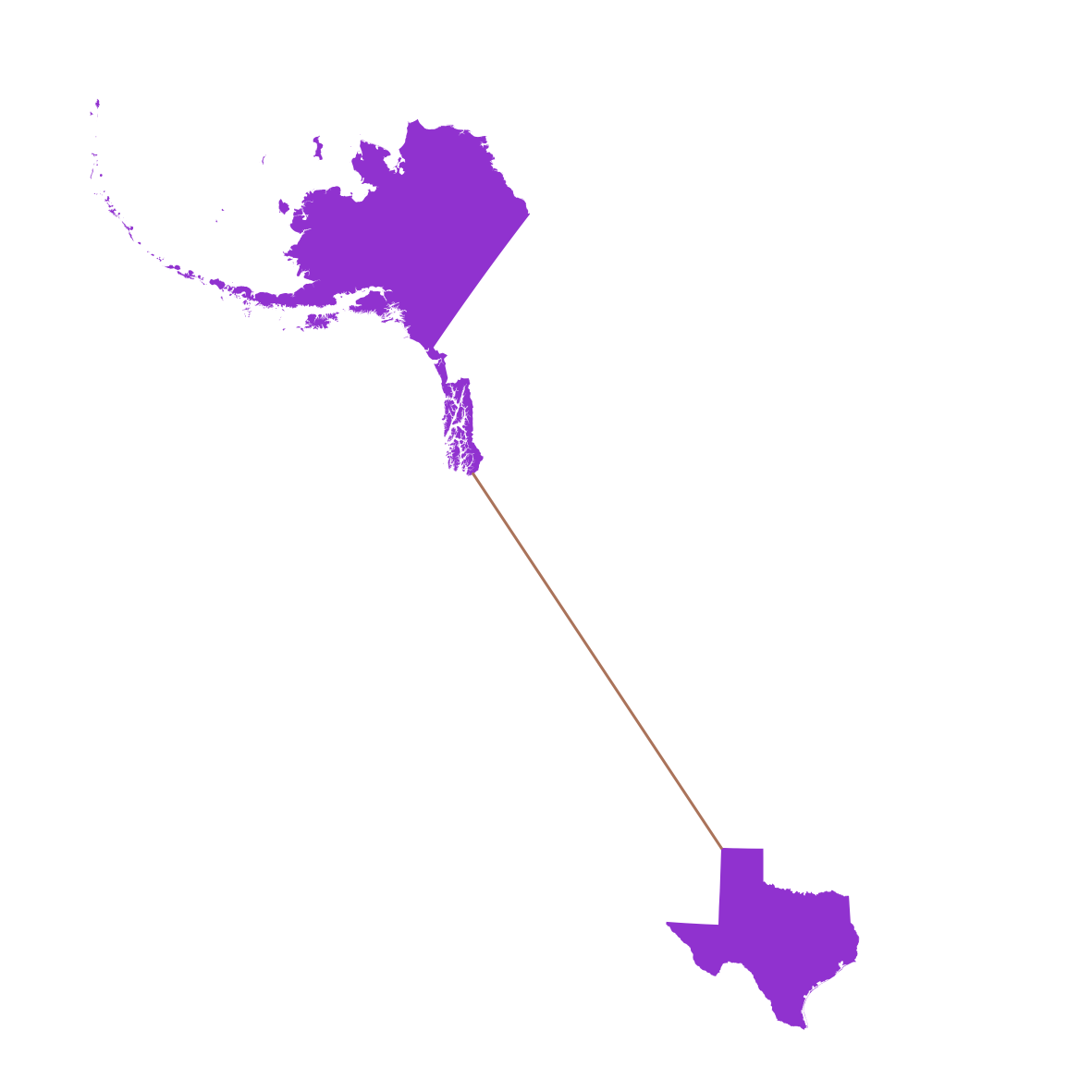
Now we are ready to calculate real distances beginning with the bounding boxes closest to each other. We continue the process until the next “min distance between bounding boxes” in our orderd list, is longer than the min distance between real geometries we have found.

The result is then the distance along a line like this returned in about 600ms.