Explanation of distance-calculation, overview ¶
The distance-calculation of today (before PostGIS 1.5) is investigating every combination of vertexes and every combination of vertex against edge in the two geometries inputed. If there is many vertexes this procedure is very heavy and slow. I have tried to find a way to narrow the distances calculated. The idea is only applicable on geometries not intersecting. Hopefully there will come up some good idea how to solve that. Until then the easiest is to check for intersecting bounding boxes (of subgeoms) and if thats the case pass it back to the old calculation.
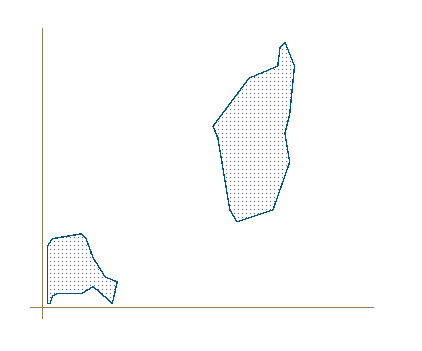
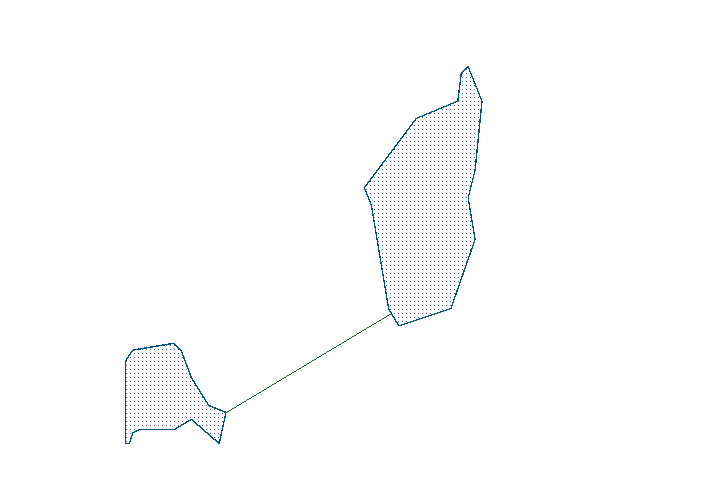
Here I will try to explain the idea in a good way. Here is two polygons that we want to calculate the smallest distance between.
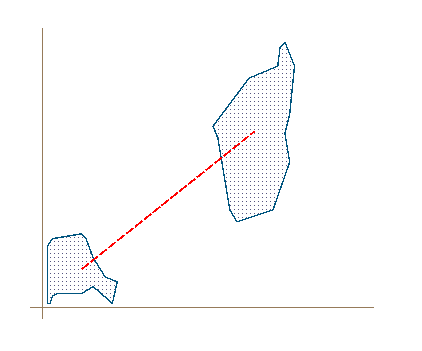
We start by finding an appropriate line between the polygons. The best one is the line between the center of the bounding boxes.
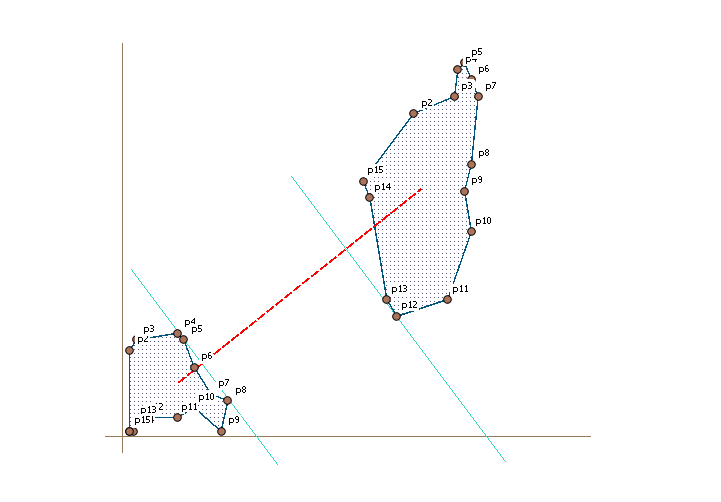
Now we want to find how every vertex is placed along this line. We illustrate this with two perpendicular lines describing p5 in polygon1 and p12 in polygon2.
Where those lines cross the x-axis gives us a value of where the points is situated along the line. We store that value for each vertex and order the vertexes by this value. P5 in polygon1 has the highest value of polygon1 and p12 has the lowest of polygon2. The first distance we calculate is between those two points. Because we not will calculate the points in ring order we have to also check the edge before and after, so we are testing polygon1 p4, p5, p6 against p11, p12, p13. That calculation will give us a shortest distance between p6 in polygon 1 and p13 in polygon2.
We now know that the distance we are searching is somewhere between the distance between the two parallel lines and the distance that we we have found between the points p6 and p13.
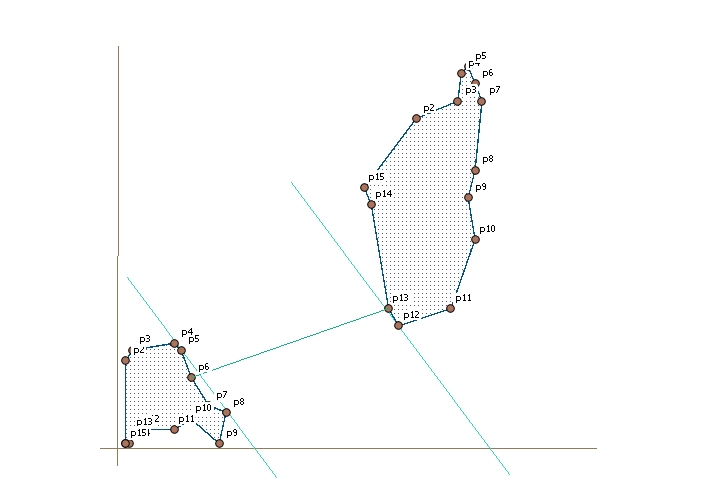
Now we take p5 from polygon1 and measure that to the points in polygon2 in order from closest to the line to more far away. We continue til we have reached the point that is that far from the left line like the shortest distance we have found that far. Then we take the next point in polygon1, p8 that is the point next closest to the line and do the same procedure, measuring against each point in polygon2 until we are «out of reach» for the already found shortest distance. This way we continue until the next point in polygon1 we are picking up is more far away from the right of the parallel lines than the shortest distance we have found. Then there can be no shorter distances to find. As mentioned earlier every check between two points include checking the point before and the point after including the edges in between.
The result is a distance calculated like described by this line from st_shortestline.
The gain from this process is that we don't have to iterate through all point. But as shown every point we actually investigate needs more calculations than todays functions because we have to search both forward and backward for each calculated point. Maybe, because of this it is wise to just use this method if the number of vertexes is more than 20 or something like that.
How this is done
This calculation is implanted instead of the array_array function when there is no intersection.
I don’t know if the letters used is international but to describe a function of a line I here use y=k*x + z
The steps are:
- Find bounding box for the two point arrays
- Check if bounding boxes intersecting. If so, send to old function
- Find center of bounding boxes and calculate deltax and deltay from the two points
- Calculate the “z” value from y=kx+z for each vertex with k-value from the slope between the two bbox-center points. To eliminate problems with dividing with zero and other limitations when getting closer to dividing with zero we instead change the x-axes with the y-axes by “mirroring” the coordinate system. In that way the “z”-value represents a lines crosspoint to the x-axes instead of the usual y-axes crossing. Hope it is understandable since I don’t know the terminology, but it works

- Now we have a list with all vertexes with this calculated “z”-values together with the ordering-value from the geometry-array.
- We order this list by the calculated “z”-value
- Now we take the two points from our list that is most close to each other according to this “z”-value and calculate the distance between them. We translate the distance value so it will be comparable with our “z”-values
- Now, we start the iteration through the vertexes. We iterate in the z-value order, which means we compare points close to the other geometry according to our z-values before we compare the values more far away. We also stop the iteration at ones the next vertex is more far away from the other geometry than our smallest found distance so far. This will narrow the search for each new mindistance we find.
Attachments (5)
- b1.png (2.9 KB ) - added by 15 years ago.
- b2.png (3.4 KB ) - added by 15 years ago.
- b3.png (12.1 KB ) - added by 15 years ago.
- b4.png (11.8 KB ) - added by 15 years ago.
- b5.png (5.0 KB ) - added by 15 years ago.
Download all attachments as: .zip