FDO RFC 59 - Support New FDO Geometry Types
This page contains a request for comments document (RFC) for the FDO Open Source project. More FDO RFCs can be found on the RFCs page.
Status
| RFC Template Version | 1.1 |
| Submission Date | April 10, 2011 |
| Last Modified | Greg Boone, April 10, 2011 |
| Author | Greg Boone |
| RFC Status | Not Ready For Review |
| Implementation Status | Not Started |
| Proposed Milestone | 3.7.0.0 |
| Assigned PSC guide(s) | Greg Boone |
| Voting History | (vote date) |
| +1 | |
| +0 | |
| -0 | |
| -1 |
Overview
Add support to the FDO Geometry API for additional parametric geometry types: Circles, Elliptical Arcs, Cubic Splines and B-Splines.
Motivation
Since the FDO API will continue to be used by new and existing clients as an interchange format, support is required for additional parametric geometry types. Specifically support for elliptical arc, cubic spline, and bspline segments. This will allow more accurate interchange of parametric geometry from client applications without having to tessellate and either lose or create ad-hoc storage for parametric geometry information.
Proposed Solution
In order to support additional Parametric Types in the FDO API, additional classes and types will need to be added to the FDO Geometry API. The following sections provide an overview of the proposed Geometry API classes and enumerations required in order to support additional parametric types.
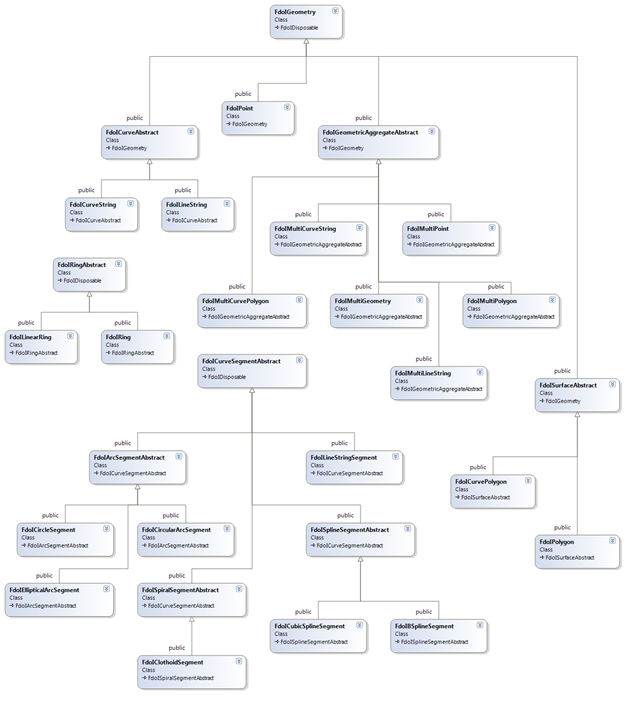
Overview of FDO API Geometry Types
Here is an overview diagram of the key FDO Geometry Interfaces and their inheritance structure. It shows the existing classes such as Point, CurveString and LineString, and the new types such as CircleSegment and EllipticalArcSegment. In combination, they decibe the major classes of the FDO Geometry API, existing and proposed
Enhanced FDO Geometry API Interfaces
The following new Geometry Segment types will be added to the FDO Geometry API to support an enhanced set of parametric geometry types.
- CircleSegment
- EllipticalArcSegment
- CubicSplineSegment
- BSplineSegment
These types work with/derive from existing types that already exist in the FDO Geometry API. Those classes act as base or sibiling classes for the types being added. The existing types include:
- CurveSegmentAbstract
- ArcSegmentAbstract
- CircularArcSegment
- LineStringSegment
Appendix “A” describes these interfaces in their API form. For additional information of the complete set of FDO Geometry API classes, refer to the online FDO API documentation, starting with the following links:
FdoIGeometry:
http://fdo.osgeo.org/files/fdo/docs/FDO_API/da/da2/class_fdo_i_geometry.htm
FdoICurveSegmentAbstract:
http://fdo.osgeo.org/files/fdo/docs/FDO_API/df/d3b/class_fdo_i_curve_segment_abstract.htm
Enum GeometryComponentType
The GeometryComponnetType enumeration will be enhanced to include enumerations for the new segment types listed above. The full enumeration is provided below, but the new types being added are as follows:
!FdoGeometryComponentType_EllipticalArcSegment
!FdoGeometryComponentType_CubicSplineSegmen
!FdoGeometryComponentType_BSplineSegment
!FdoGeometryComponentType_CircleSegment
This enumeration applies to certain helper types that are used to compose other types which derive from FdoIGeometry.
enum FdoGeometryComponentType
{
/// LinearRing type (FdoILinearRing).
FdoGeometryComponentType_LinearRing = 129,
/// CircularArcSegment type (FdoICircularArcSegment).
FdoGeometryComponentType_CircularArcSegment = 130,
/// LineStringSegment type (FdoILineStringSegment).
FdoGeometryComponentType_LineStringSegment = 131,
/// Ring type (FdoIRing).
FdoGeometryComponentType_Ring = 132,
/// EllipticalArcSegment type (FdoIEllipticalArcSegment).
FdoGeometryComponentType_EllipticalArcSegment = 133,
/// CubicSplineSegment type (FdoICubicSplineSegment).
FdoGeometryComponentType_CubicSplineSegment = 135,
/// BSplineSegment type (FdoIBSplineSegment).
FdoGeometryComponentType_BSplineSegment = 136,
/// CircleSegment type (FdoICircleSegment).
FdoGeometryComponentType_CircleSegment = 137
};
Class FdoIEllipticalArcSegment
The FdoIEllipticalArcSegment class represets an Elliptical Arc Segment geometry type. EllipticalArcSegment can describe portions of, or a full ellipse. If describing a full ellipse, the start and end points are identical and the mid-point is the diametrically opposite point on the ellipse.
Two foci were specified as opposed to major/minor axes so that the API can derive this class from ArcSegmentAbstract and CurveSegmentAbstract, thus reusing the concepts of start/mid/end points as defined in the base classes. In this manner the API can maintain a common look/feel when defining arc types. The expectation is that a Geometry API utility method will be provided that will allow conversion to major/minor axis.
The semimajor axis and the semiminor axis are one half of the major and minor diameters, respectively. These are sometimes called the major and minor semi-axes, the major and minor semiaxes,or major radius and minor radius.
The foci of the ellipse are two special points on the ellipse's major axis and are equidistant from the center point. The sum of the distances from any point on the ellipse to those two foci is constant and equal to the major diameter. Each of these two points is called a focus of the ellipse.
class FdoIEllipticalArcSegment : public FdoIArcSegmentAbstract
{
public:
/// \brief
/// Gets the two focal positions of this Ellipse Geometry.
///
/// \return
/// Returns the two focal positions of the Ellipse as a collection
/// of two positions.
///
virtual FdoIDirectPositionCollection const * GetFocalPositions() const = 0;
/// \brief
/// Gets the two focal positions of this Ellipse Geometry as an array.
/// The ordinates are in the order XYZMXYZM, with only those present
/// according to the dimensionality.
///
/// \return
/// Returns the two focal positions of the Ellipse as a collection
///
virtual const double * GetFocalPositionOrdinates() = 0;
};
Class FdoICircleSegment
The FdoICircleSegment class represents a circle as an arc whose ends coincide to form a simple closed loop. The three control positions shall be distinct non-co-linear positions for the circle to be unambiguously defined. The arc is simply extended past the third control position until the first control position is encountered.
Circle segments cannot be defined as non-closed segments. If describing a circle where the start and end points are identical the mid-point is the diametrically opposite point on the circle.
class FdoICircleSegment : public FdoIArcSegmentAbstract
{
protected:
/// \brief
/// Constructs a default instance.
///
FdoICircleSegment() {};
/// \brief
/// Default destructor.
///
virtual ~FdoICircleSegment() {};
};
Class FdoISpiralSegmentAbstract
The FdoISpiralSegmentAbstract class represets a Spiral curve segment (abstract). ISpiralSegmentAbstract is the based class for all spline geometry types, including cubic-splaine and b-spline.
class FdoISpiralSegmentAbstract : public FdoICurveSegmentAbstract
{
public:
/// \brief
/// Gets the clockwise state from this spiral segment.
///
/// \return
/// Returns true if the spiral is defined clockwise, otherwise false
///
virtual bool GetIsClockwise() const = 0;
};
Class FdoISplineSegmentAbstract
The FdoISplineSegmentAbstract class is the base class for Spline segments (abstract). ISplineSegmentAbstract is the based class for all spline geometry types, including cubic-splaine and b-spline.
class FdoISplineSegmentAbstract : public FdoICurveSegmentAbstract
{
public:
/// \brief
/// Gets the algebraic degree of the spline's basis function.
/// The spline's degree is a positive integer that is the degree
/// of the polynomial equations used to calculate the pieces of
/// the spline. For Cubic splines, the degree is fixed at 3.
///
/// \return
/// Returns an interger specifying the spline's degree value
///
virtual FdoInt32 GetDegree() const = 0;
/// \brief
/// Gets the the interpolation mechanism for a spline Geometry.
/// Is fixed as Cubic for Cubic splines. Can be polynomial or
/// Rational for B-Splines.
///
/// \return
/// Returns the interpolation mechanism used to create the spline
///
virtual FdoGeometricInterpolationType GetInterpolationType() const = 0;
/// \brief
/// Gets the collection of control position associated to this Spline Geometry.
///
/// \return
/// Returns the collection of control positions associated to the spline
///
virtual FdoDirectPositionCollection const* GetControlPositions() const = 0;
/// \brief
/// Gets the number of control positions associated to this Spline geometry.
///
/// \return
/// Returns the control position count
///
virtual FdoInt32 GetControlPositionCount() const = 0;
/// \brief
/// Gets a control position at the specified (zero-based) index.
///
/// \param index
/// Input Zero-based index in the Spline's list of control positions.
///
/// \return
/// Returns the control position position at the specified index
///
virtual FdoIDirectPosition const* GetControlPosition(FdoInt32 index) const = 0;
/// \brief
/// Gets the control position at the specified (zero-based) index,
/// by values of its member data.
/// This is in aid of higher performance for any implementation that
/// does not internally use FdoIDirectPosition objects for storage, or for
/// an application seeking to avoid overhead of accessor methods.
///
/// \param index
/// Input Zero-based index in the object's list of control positions.
/// \param x
/// Output X ordinate value.
/// \param y
/// Output Y ordinate value.
/// \param z
/// Output Z ordinate value.
/// \param m
/// Output M ordinate value.
/// \param dimensionality
/// Output Dimensionality of ordinates in this control position.
///
/// \return
/// Returns nothing
///
virtual void GetControlPositionByMembers(
FdoInt32 index,
double *x,
double *y,
double *z,
double *m,
FdoInt32 *dimensionality) const = 0;
/// \brief
/// Gets the spline control positions as an array.
///
/// \remarks
/// The caller must not free the returned array.
/// The ordinates are in the order XYZMXYZM..., with only those present
/// according to the dimensionality.
///
/// \return
/// Returns the spline's control positions ordinates
///
virtual const double * GetControlPositionOrdinates() = 0;
};
Class FdoICubicSplineSegment
The FdoICubicSplineSegment class is a Cubic Spline geometry type. A cubic spline is a spline constructed of piecewise third-order polynomials which pass through a set of control positions. The second derivative of each polynomial is commonly set to zero at the end position, since this provides a boundary condition that completes the system of equations.
class FdoICubicSplineSegment : public FdoISplineSegmentAbstract
{
public:
/// \brief
/// Gets the unit tangent vector at the start position of the spline.
/// Only the direction of the vectors shall be used to determine
/// the shape of the cubic spline, not their length.
///
/// \return
/// Returns the tangent vector
///
virtual FdoIDirectPosition const * GetStartTangent() const = 0;
/// \brief
/// Gets the unit tangent vector at the end position of the spline.
/// Only the direction of the vectors shall be used to determine
/// the shape of the cubic spline, not their length.
///
/// \return
/// Returns the tangent vector
///
virtual FdoIDirectPosition const * GetEndTangent() const = 0;
};
Enum GeometricKnotTypes
Enumeration used to identify the B-spline knot type used to ineterpolate a B-Spline.
A B-spline is uniform if and only if all knots are of multiplicity 1 and they differ by a positive constant from the preceding knot.
A B-spline is quasi-uniform if and only if the knots are of multiplicity (degree+1) at the ends, of multiplicity 1 elsewhere, and they differ by a positive constant from the preceding knot. In general, in a piecewise Bezier knot vector, the first k knots are the same, then each subsequent group of k-1 knots is the same, until you get to the end. Note that a piecewise Bézier curve must have nk–1 control positions, where n is the number of segments (i.e., the number of control positions is one less than an even multiple of the order).
enum FdoGeometricKnotType
{
/// The knots are appropriate for a uniform B-spline.
FdoGeometricKnotType_Uniform = 500,
/// The knots are appropriate for a quasi-uniform B-spline.
FdoGeometricKnotType_QuasiUniform = 501,
/// The knots are appropriate for a piecewise Bezier curve.
FdoGeometricKnotType_PiecewiseBezier = 502,
};
Class FdoIBSplineKnot
Class FdoIBSplineKnot controls the constructive parameter space for spline curves. Each knot sequence is used for a dimension of the spline's parameter space.
class FdoIBSplineKnot : public FdoIDisposable
{
public:
/// \brief
/// Gets the value of the parameter at the knot of the spline.
/// The sequence of knots shall be a nondecreasing sequence.
/// That is, each knot's value in the sequence shall be equal
/// to or greater than the previous knot's value. The use of
/// equal consecutive knots is normally handled using the
/// multiplicity.
///
/// \return
/// Returns the knot parameter
///
virtual double GetValue() const = 0;
/// \brief
/// Gets The value of the averaging weight used for this
/// knot of the spline
///
/// \return
/// Returns the knot weight
///
virtual double GetWeight() const = 0;
/// \brief
/// Gets the multiplicity of this knot used in the definition of
/// the spline (with the same weight).
///
/// \return
/// Returns the knot multiplicity
///
virtual FdoInt32 GetMultiplicity() const = 0;
};
Class FdoBSplineKnotCollection
The FdoBSplineKnotCollection class is a simple collection of FdoIBSplineKnot objects.
class FdoBSplineKnotCollection : public FdoCollection<FdoIBSplineKnot, FdoException>
{
public:
/// \brief
/// Creates an instance of FdoBSplineKnotCollection with no contained elements.
///
/// \return
/// Returns an empty collection
///
static FdoBSplineKnotCollection* Create();
};
Class FdoIBSplineSegment
The FdoIBSplineSegment class is a B-Spline geometry type. A B-Spline is a piecewise parametric polynomial or rational curve described in terms of control positions and basis functions. The interpolation method may be either "polynomial" or "rational" depending on the interpolation type; default is "polynomial".
class FdoIBSplineSegment : public FdoISplineSegmentAbstract
{
public:
/// \brief
/// Determines in the B-Spline is a polynomial spline
///
/// \return
/// Returns true if the Spline is polynomial, otherwise false
///
virtual bool GetIsPolynomial() const = 0;
/// \brief
/// Gets the knot type of the B-Spline
///
/// \return
/// Returns the knot type as an FdoGeometricKnotType enumeration
///
virtual FdoGeometricKnotType GetKnotType() const = 0;
/// \brief
/// Gets the collection of knots associated to this Spline Geometry.
///
/// \return
/// Returns the collection of knots associated to the spline
///
virtual FdoBSplineKnotCollection const* GetKnots() const = 0;
/// \brief
/// Gets the number of knots associated to this Spline geometry.
///
/// \return
/// Returns the knot count
///
virtual FdoInt32 GetKnotCount() const = 0;
/// \brief
/// Gets a knot at the specified (zero-based) index.
///
/// \param index
/// Input Zero-based index in the Spline's list of knots.
///
/// \return
/// Returns the knot at the specified index
///
virtual FdoIBSplineKnot const* GetKnot(FdoInt32 index) const = 0;
/// \brief
/// Gets the knot at the specified (zero-based) index, by values of
/// its member data. This is in aid of higher performance for any
/// implementation that does not internally use knot objects for storage,
/// or for an application seeking to avoid overhead of accessor methods.
///
/// \param index
/// Input Zero-based index in the object's list of control positions.
/// \param value
/// Output knot value.
/// \param weight
/// Output knot weight.
/// \param multiplicity
/// Output the mutiplicity of the knot.
///
/// \return
/// Returns nothing
///
virtual void GetKnotByMembers(
FdoInt32 index,
double *value,
double *weight,
FdoInt32 *multiplicity) const = 0;
};
Additions to the Geometry Factory Class
The GeometryFactoryAbstract class is a factory (abstract, non-pure) for Geometry objects and Geometry helper objects. The methods described below will be added to the definition of the Factory Class.
class FdoGeometryFactoryAbstract : public FdoIDisposable
{
public:
/// EllipticalArcSegment
/// \brief
/// Creates a EllipticalArcSegment object by specifying three
/// points on the arc, and the two focal positions.
///
/// \param startPosition
/// Input starting position of the ellipse
/// \param midPosition
/// Input a position on the ellipse, and not equal to the starting
/// or ending positions
/// \param endPosition
/// Input ending position of the ellipse
/// \param focalPoisition1
/// Input the first focal position of the ellipse
/// \param focalPoisition2
/// Input the second focal position of the ellipse
///
/// \return
/// Returns an EllipticalArc Segment
///
virtual FdoIEllipticalArcSegment* CreateEllipticalArcSegment(
FdoIDirectPosition* startPosition,
FdoIDirectPosition* midPosition,
FdoIDirectPosition* endPosition,
FdoIDirectPosition* focalPoisition1,
FdoIDirectPosition* focalPoisition2) = 0;
/// CircleSegment
/// \brief
/// Creates a CircleSegment object using three points on the circle.
///
/// \param firstPosition
/// Input first position of the circle
/// \param secondPosition
/// Input a position on the circle, and not equal to the first or third positions
/// \param thirdPosition
/// Input third position of the circle
///
/// \return
/// Returns a CircleSegment
///
FDO_GEOM_API virtual FdoICircleSegment* CreateCircleSegment(
FdoIDirectPosition* firstPosition,
FdoIDirectPosition* secondPosition,
FdoIDirectPosition* thirdPosition) = 0;
/// SplineSegments
/// \brief
/// Creates a Cubic Spline segment from the start and end tangents,
/// and a set of control positions
///
/// \param startTangent
/// Input the start tanget of the spline
/// \param endTangent
/// Input the end tanget of the spline
/// \param controlPositions
/// Input the collection of control positions that define the spline
/// \return
/// Returns a Cubic Spline Segment
///
virtual FdoICubicSplineSegment* CreateCubicSplineSegment(
FdoIDirectPosition* startTangent,
FdoIDirectPosition* endTangent,
FdoDirectPositionCollection* controlPositions) = 0;
/// \brief
/// Creates a B-Spline segment from collections of
/// control positions and knots,
///
/// \param degree
/// Input the algebraic degree of the basis function.
/// \param controlPositions
/// Input the control positions that will be used to contruct the spline
/// \param knots
/// Input the knots that will be used to contruct the spline
/// \param weights
/// \param knotType
/// Input the knotType to be used to contruct the spline
///
/// \return
/// Returns a B-Spline Segment
///
virtual FdoIBSplineSegment* CreateBSplineSegment(
FdoInt32 degree,
FdoDirectPositionCollection* controlPositions,
FdoBSplineKnotCollection* knots,
FdoGeometricKnotType knotType) = 0; /// KnotType: TDB
};
FGF Text Definitions
The following FGF Text definitions will be supported by the FDO API for the new types specified above.
EllipticalArc Segment
ELLIPTICALARCSEGMENT (
[Mid Position],
[End Position],
[Focal Point 1],
[Focal Point 2]
)
Example
CURVESTRING XYZ (0 0 0 (
CIRCULARARCSEGMENT (0 1 0, 1 2 0),
LINESTRINGSEGMENT (3 0 0, 3 2 0),
ELLIPTICALARCSEGMENT (-1 1 0, 1 3 0, 2 0 0, 3 0 0)
))
Circle Segment
CIRCLESEGMENT (
[Mid Position],
[End Position]
)
Example
CURVESTRING XYZ (0 0 0 (
CIRCLESEGMENT (-1 1 0, 1 3 0)
))
CubicSpline Segment
CUBICSPLINESEGMENT (
[Position Count],
[Position 1],
...
[Position n]
[Start Tangent],
[End Tangent]
)
Example
CURVESTRING XYZ (0 0 0 (
LINESTRINGSEGMENT (7.5 0 0, 11.5 4 0),
CIRCULARARCSEGMENT (13 7.5, 12.5 12 0),
CUBICSPLINESEGMENT (2, 5 15 0, 6 19 0, 0 0 0, 0 0 0)
))
BSpline Segment
BSPLINESEGMENT (
[Degree],
[Position Count],
[Position 1],
...
[Position n],
[Knot Count],
[Value 1] [Weight 1] [Multiplicity 1],
...
[Value n] [Weight n] [Multiplicity n]
)
Example
CURVESTRING XYZ (0 0 0 (
LINESTRINGSEGMENT (7.5 0 0, 11.5 4 0),
CIRCULARARCSEGMENT (13 7.5, 12.5 12 0),
BSPLINESEGMENT (4,
6,
11.98 12.74 0,
11.46 13.48 0,
8.86 16.57 0,
5.74 14 0,
3.08 10.18 0,
-1.06 11.62 0,
4,
0 1 4,
1 1 1,
2 1 1,
3 1 4)
))
FGF Binary Definitions
The following FGF Binary definitions will be supported by the FDO API for the new types specified above.
Basic Type Definitions
Point {
double x;
double y
};
PointZ {
double x;
double y;
double z
};
PointM {
double x;
double y;
double m
};
PointZM {
double x;
double y;
double z;
double m
};
Position ::= Point | PointZ | PointM | PointZM;
Vector ::= Point | PointZ;
Tangent ::= Point | PointZ;
Knot Type Definitions
Knot {
double value;
double weight;
uint32 multiplicity;
};
EllipticalArc Segment
ELLIPTICALARCSEGMENT {
static uint32 FGFBType = 133;
Position midPosition;
Position endPosition;
Position focalPosition1;
Position focalPosition2;
};
Circle Segment
CIRCLESEGMENT {
static uint32 FGFBType = 137;
Position firstPosition;
Position secondPosition;
Position thirdPosition1;
};
CubicSpline Segment
CUBICSPLINESEGMENT {
static uint32 FGFBType = 135;
uint32 numPositions;
Position positions[numPositions];
Tangent startTangent;
Tangent endTangent;
);
BSpline Segment
BSPLINESEGMENT {
static uint32 FGFBType = 136;
uint32 degree;
uint32 numPositions;
Position positions[numPositions];
uint32 numKnots;
Knot knots[numKnots];
};
GeometryFactory Examples
Elliptical Arc Segment Example
FdoICurveString* CreateCurveString()
{
// Create and return a curve string consisting of
// one elliptical arc segment
// one linear string segment
// line segment = (0 0 0), (3 0 0), (3 2 0)
FdoPtr<FdoFgfGeometryFactory> gf = FdoFgfGeometryFactory::GetInstance();
FdoPtr<FdoDirectPositionCollection> points = FdoDirectPositionCollection::Create();
FdoPtr<FdoIDirectPosition> pt1 = gf->CreatePositionXY(0.0, 0.0);
FdoPtr<FdoIDirectPosition> pt2 = gf->CreatePositionXY(3.0, 0.0);
FdoPtr<FdoIDirectPosition> pt3 = gf->CreatePositionXY(3.0, 2.0);
points->Add(pt1);
points->Add(pt2);
points->Add(pt3);
FdoPtr<FdoILineStringSegment> lineSeg = gf->CreateLineStringSegment(points);
// elliptical segment = (3 2 0), (-1 1 0), (1 3 0), (2 0 0), (3 0 0)
FdoPtr<FdoIDirectPosition> startPos = gf->CreatePositionXY(3.0, 2.0);
FdoPtr<FdoIDirectPosition> midPos = gf->CreatePositionXY(-1.0, 1.0);
FdoPtr<FdoIDirectPosition> endPos = gf->CreatePositionXY(1.0, 3.0);
FdoPtr<FdoIDirectPosition> focalPos1 = gf->CreatePositionXY(2.0, 0.0);
FdoPtr<FdoIDirectPosition> focalPos2 = gf->CreatePositionXY(3.0, 0.0);
FdoPtr<FdoIEllipticalArcSegment> arcSeg = gf->CreateEllipticalArcSegment(
startPos,
midPos,
endPos,
focalPos1,
focalPos2);
FdoPtr<FdoCurveSegmentCollection> curveSegs = FdoCurveSegmentCollection::Create();
curveSegs->Add(lineSeg);
curveSegs->Add(arcSeg);
FdoPtr<FdoICurveString> curveString = gf->CreateCurveString(curveSegs);
CheckFGFT(curveString, L"CURVESTRING (0 0 ("
L"LINESTRINGSEGMENT (3 0, 3 2),"
L"ELLIPTICALARCSEGMENT (-1 1, 1 3, 2 0, 3, 0)"
L"))");
return FDO_SAFE_ADDREF(curveString.p);
}
Circle Segment Example
FdoICurveString* CreateCurveString()
{
// Create and return a curve string consisting of
// one circle segment
// circle segment = (0 0 0), (-1 1 0), (1 3 0)
FdoPtr<FdoIDirectPosition> pt1 = gf->CreatePositionXY(0.0, 0.0);
FdoPtr<FdoIDirectPosition> pt2 = gf->CreatePositionXY(-1.0, 1.0);
FdoPtr<FdoIDirectPosition> pt3 = gf->CreatePositionXY(1.0, 3.0);
FdoPtr<FdoICircleSegment> circleSeg = gf->CreateCircleSegment(
pt1,
pt2,
pt3);
FdoPtr<FdoCurveSegmentCollection> curveSegs = FdoCurveSegmentCollection::Create();
curveSegs->Add(circleSeg);
FdoPtr<FdoICurveString> curveString = gf->CreateCurveString(curveSegs);
CheckFGFT(curveString, L"CURVESTRING (0 0 ("
L"CIRCLESEGMENT (-1 1, 1 3)"
L"))");
return FDO_SAFE_ADDREF(curveString.p);
}
Cubic Spline Segment Example
FdoICurveString* CreateCurveString()
{
// Create and return a curve string consisting of:
// one linear string segment
// one circular arc segment
// one cubic spline segment
// line segment = (0 0 0), (7.5 0 0), (11.5 4 0)
FdoPtr<FdoFgfGeometryFactory> gf = FdoFgfGeometryFactory::GetInstance();
FdoPtr<FdoDirectPositionCollection> points = FdoDirectPositionCollection::Create();
FdoPtr<FdoIDirectPosition> pt1 = gf->CreatePositionXY(0.0, 0.0);
FdoPtr<FdoIDirectPosition> pt2 = gf->CreatePositionXY(7.5, 0.0);
FdoPtr<FdoIDirectPosition> pt3 = gf->CreatePositionXY(11.5, 4.0);
points->Add(pt1);
points->Add(pt2);
points->Add(pt3);
FdoPtr<FdoILineStringSegment> lineSeg = gf->CreateLineStringSegment(points);
// circular arc segment = (11.5 4 0), (13 7.5 0), (12.5 12 0)
FdoPtr<FdoIDirectPosition> startPos = gf->CreatePositionXY(11.5, 4.0);
FdoPtr<FdoIDirectPosition> midPos = gf->CreatePositionXY(13.0, 7.5);
FdoPtr<FdoIDirectPosition> endPos = gf->CreatePositionXY(12.5, 12.0);
FdoPtr<FdoICircularArcSegment> arcSeg = gf->CreateCircularArcSegment(
startPos, midPos, endPos);
// cubic spline segment = (8 3 0), (5 15 0), (6 19 0), (0 0 0), (0 0 0)
FdoPtr<FdoDirectPositionCollection> cntrlptColl = FdoDirectPositionCollection::Create();
FdoPtr<FdoIDirectPosition> cntrlpt1 = gf->CreatePositionXY(8.0, 3.0);
FdoPtr<FdoIDirectPosition> cntrlpt2 = gf->CreatePositionXY(5.0, 15.0);
FdoPtr<FdoIDirectPosition> cntrlpt3 = gf->CreatePositionXY(6.0, 19.0);
cntrlptColl-Add(cntrlpt1);
cntrlptColl-Add(cntrlpt2);
cntrlptColl-Add(cntrlpt3);
FdoPtr<FdoIDirectPosition> startTan = gf->CreatePositionXY(0.0, 0.0);
FdoPtr<FdoIDirectPosition> endTan = gf->CreatePositionXY(0.0, 0.0);
FdoPtr<FdoICubicSplineSegment> splineSeg = gf->CreateCubicSplineSegment(
cntrlptColl,
startTan,
endTan);
FdoPtr<FdoCurveSegmentCollection> curveSegs = FdoCurveSegmentCollection::Create();
curveSegs->Add(lineSeg);
curveSegs->Add(arcSeg);
curveSegs->Add(splineSeg);
FdoPtr<FdoICurveString> curveString = gf->CreateCurveString(curveSegs);
CheckFGFT(curveString, L"CURVESTRING XYZ (0 0 0 ("
L"LINESTRINGSEGMENT (7.5 0 0, 11.5 4 0),"
L"CIRCULARARCSEGMENT (13 7.5 0, 12.5 12 0),"
L"CUBICSPLINESEGMENT (2, 5 15 0, 6 19 0, 0 0 0, 0 0 0)"
L"))"
return FDO_SAFE_ADDREF(curveString.p);
}
Appendix A: Existing FDO API Curve Segment Classes
The classes described in the following sections currently exist in the FDO Geometry API (Version 3.6.0) and form base and sibling classes to those proposed in the sections above. They are included here for illustrative and comparative purposes.
ICurveSegmentAbstract
The FdoICurveSegmentAbstract class is an abstract geometric Curve Segment object. This class is used strictly as a component of curves and, thus, does not inherit from IGeometry.
class FdoICurveSegmentAbstract : public FdoIDisposable
{
public:
/// \brief
/// Gets the envelope for the curve segment.
///
/// \return
/// Returns the envelope
///
FDO_GEOM_API virtual FdoIEnvelope* GetEnvelope() const = 0;
/// \brief
/// Gets the starting position of this curve segment.
///
/// \return
/// Returns the starting position
///
FDO_GEOM_API virtual FdoIDirectPosition* GetStartPosition() const = 0;
/// \brief
/// Gets the ending position of this curve segment.
///
/// \return
/// Returns the ending position
///
FDO_GEOM_API virtual FdoIDirectPosition* GetEndPosition() const = 0;
/// \brief
/// Gets the closure state for the curve segment.
///
/// \remarks
/// The meaning behind this method is not guaranteed
/// to be uniform between derived types or between implementations
/// of this package. It may represent a computed value, an explicit
/// attribute, or be true by definition. As a computed value, the
/// result is typically from simply testing the starting and
/// ending positions for exact equality. This is only reliable in floating
/// point arithmetic if these data have identical origins.
/// As an explicit attribute, it would be persisted with the Geometry and
/// typically denoted by a parameter in the relevant factory method.
/// Some Geometry types are closed by definition.
///
/// \return
/// Returns 'true' if the curve is closed, and false otherwise
///
FDO_GEOM_API virtual bool GetIsClosed() const = 0;
/// \brief
/// Gets the type of the most-derived interface
/// in the Geometry package for this object
///
/// \return
/// Returns the derived type
///
FDO_GEOM_API virtual FdoGeometryComponentType GetDerivedType() const = 0;
/// \brief
/// Gets the dimensionality of ordinates in this object.
///
/// \remarks
/// Values are from the FdoDimensionality enumeration.
/// A return type of "FdoInt32" is used instead of the enumeration,
/// catering to typical use with bit masking.
///
/// \return
/// Returns the ordinate dimensionality
///
FDO_GEOM_API virtual FdoInt32 GetDimensionality() const = 0;
};
IArcSegmentAbstract
The FdoIArcSegmentAbstract class is an arc curve segment (abstract)
class FdoIArcSegmentAbstract : public FdoICurveSegmentAbstract
{
public:
/// \brief
/// Gets some position along the curve, between the starting and ending positions.
///
/// \remarks
/// Depending on the derived type and its implementation, this may be a
/// computed value, or a persisted value used as part
/// of the definition of the curve segment. This position is the only
/// means to deduce the curve segment's orientation in some cases, such as
/// when it is closed or vertically aligned ('on edge' when looking along
/// the Z axis).
///
/// \return
/// Returns a midpoint on the curve
///
FDO_GEOM_API virtual FdoIDirectPosition* GetMidPoint() const = 0;
};
ICircularArcSegment
The FdoICircularArcSegment class is a circular arc curve segment
class FdoICircularArcSegment : public FdoIArcSegmentAbstract
{
protected:
/// \brief
/// Default destructor.
///
/// \return
/// Returns nothing
///
FDO_GEOM_API virtual ~FdoICircularArcSegment() {};
};
ILineStringSegment
The FdoILineStringSegment class is a LineString curve segment type. The shape of FdoILineStringSegment is the set of positions defined by the contained collection, plus linear interpolation between consecutive points. This is a helper type for Geometries in the Geometry package.
Note: It does not derive from IGeometry.
class FdoILineStringSegment : public FdoICurveSegmentAbstract
{
public:
/// \brief
/// Gets the number of positions in this object.
///
/// \return
/// Returns the number of positions
///
FDO_GEOM_API virtual FdoInt32 GetCount() const = 0;
/// \brief
/// Gets the position at the specified (zero-based) index.
///
/// \return
/// Returns the position
///
FDO_GEOM_API virtual FdoIDirectPosition* GetItem(FdoInt32 index) const = 0;
/// \brief
/// Gets a collection of all of the positions in this object.
///
/// \return
/// Returns the positions
///
FDO_GEOM_API virtual FdoDirectPositionCollection* GetPositions() = 0;
/// \brief
/// Gets the ordinates as an array.
///
/// \remarks
/// The caller must not free the returned array.
/// The ordinates are in the order XYZMXYZM..., with only those present
/// according to the dimensionality.
///
/// \return
/// Returns the ordinates
///
FDO_GEOM_API virtual const double * GetOrdinates() = 0;
};
Appendix B: Questions and Answers
ICircleSegment vs. ICircle
Question:
What if we change the proposal to derive FdoICircleSegment directly from FdoICurveAbstract, in the process renaming FdoICircleSegment to be FdoICircle. To me, this has some merit, since as currently described, a circle must be closed and cannot be combined with any other ArcSegment Types to form complex curve strings. They can only stand alone, and wrapping it in a CurveString seems wasteful. If a user wished to define a non-closed circle, they would use ICircularArcSegment.
Response:
The FdoICircle may be something of a hard sell. In OGC, Circle extends Arc, which extends ArcString, which extends CurveSegment, which implements GenericCurve.
Can ICircularArcSegment Describe a Closed Circle
Question:
I’m not sure how CircularArcSegment can describe a full circle. If the start and end points are identical, then you only have two points (start/end and mid-point), which does not define the plane of the arc for XYZ dimensionality.
Response:
For the rest of this explanation, it’s assumed that the circle is complete (start and end are same position).
Take the line that is formed by the start and mid positions. The normal to that line in the XY plane forms another line through the circle to orient it. The circle is treated as if you simply tilted it out of the XY plane by grabbing the mid position.
There is a position of ambiguity: if the circle is standing perfectly on edge so that the start and mid positions coincide in XY (but have different Z).
This (using an FDO circle in 3D) works for round-tripping and a few special functions such as tessellation. However, there are several weak points in GIS applications that assume circular arcs to be in the XY plane. These should be addressed by the time that they add support for more geometry types, assuming that 3D support will be required for all of them.
Appendix C: OGC WKT vs FGF WKT
The following analysis is based on the examination of the OGC WKB format vs. the As-Implemented FGF WKB format in FDO 3.5.0. The most recent OGC WKB Specification can be located at the following link. Refer to Section 7 on Page 53: “Well-known Text Representation for Geometry”.
OpenGIS Implementation Specification for Geographic information - Simple feature access
In general FGF WKT is a superset of WKT, and includes geometry types that are not yet fully defined by a WKB specification. While FGF will continue to be a superset of WKT, the following sections outline areas where further alignment can be made.
Dimensionality
In FGF WKT, where the dimensionality of the geometry is not XY, The following string values are written:
| Dimensionality | Text |
| XYZ | XYZ |
| XYM | XYM |
| XYZM | XYZM |
In OGC WKT, where the dimensionality of the geometry is not XY, The following string values are expected to be written to the string:
| Dimensionality | Text |
| XYZ | Z |
| XYM | M |
| XYZM | ZM |
Appendix D: OGC WKB vs FGF WKB
The following analysis is based on the examination of the OGC WKB format vs. the As-Implemented FGF WKB format in FDO 3.5.0. The most recent OGC WKB Specification can be located at the following link. Refer to Section 8 on Page 63: “Well-known Binary Representation for Geometry”.
OpenGIS Implementation Specification for Geographic information - Simple feature access
In general FGF WKB is a superset of WKB, and includes geometry types that are not yet fully defined by a WKB specification. While FGF will continue to be a superset of WKB, the following sections outline areas where further alignment can be made.
Byte Order
The OGC WKB specification states that the Byte Oder is written out as a part of a geometric WKB Definition.
"The [OGC] Well-known Binary Representation for Geometry is obtained by serializing a geometric object as a sequence of numeric types drawn from the set {Unsigned Integer, Double} and then serializing each numeric type as a sequence of bytes using one of two well defined, standard, binary representations for numeric types (NDR, XDR). The specific binary encoding (NDR or XDR) used for a geometry representation is described by a one-byte tag that precedes the serialized bytes. The only difference between the two encodings of geometry is one of byte order, the XDR encoding is Big Endian, and the NDR encoding is Little Endian."
FGF WKB does not write out binary encoding for NDR/XDR. FDO expects all WKB it processes to be in a Little-Endian format.
Common List of Codes for Geometric Types
The OGC WKB standard defines a common list of codes for geometric types. These types not only indicate the geometric types, but also the dimensionality of the type. Thus a single integer is defined to represent both pieces of information.
FGF WKB writes out the geometric type and dimensionality information as two integers, one for the geometric type and another for the dimensionality. The geometric values used are a basic subset of the OGC WKB values, specifically those used to represent XY geometries.
FGF Geometric Types
The following are a list of FGF Geometry Types
| Type | Code |
| Geometry | 0 |
| Point | 1 |
| LineString | 2 |
| Polygon | 3 |
| MultiPoint | 4 |
| MultiLineString | 5 |
| MultiPolygon | 6 |
| MultiGeometry | 7 |
| CurveString | 10 |
| CurvePolygon | 11 |
| MultiCurveString | 12 |
| MultiCurvePolygon | 13 |
WKB Geometric Types
The following tables list the WKB Geometry Types and their associated codes.
| Type | Code |
| Geometry | 0 |
| Point | 1 |
| LineString | 2 |
| Polygon | 3 |
| MultiPoint | 4 |
| MultiLineString | 5 |
| MultiPolygon | 6 |
| GeometryCollection | 7 |
| CircularString | 8 |
| CompoundCurve | 9 |
| CurvePolygon | 10 |
| MultiCurve | 11 |
| MultiSurface | 12 |
| Curve | 13 |
| Surface | 14 |
| PolyhedralSurface | 15 |
| TIN | 16 |
| Type | Code |
| Geometry Z | 1000 |
| Point Z | 1001 |
| LineString Z | 1002 |
| Polygon Z | 1003 |
| MultiPoint Z | 1004 |
| MultiLineString Z | 1005 |
| MultiPolygon Z | 1006 |
| GeometryCollection Z | 1007 |
| CircularString Z | 1008 |
| CompoundCurve Z | 1009 |
| CurvePolygon Z | 1010 |
| MultiCurve Z | 1011 |
| MultiSurface Z | 1012 |
| Curve Z | 1013 |
| Surface Z | 1014 |
| PolyhedralSurface Z | 1015 |
| TIN Z | 1016 |
| Type | Code |
| Geometry M | 2000 |
| Point M | 2001 |
| LineString M | 2002 |
| Polygon M | 2003 |
| MultiPoint M | 2004 |
| MultiLineString M | 2005 |
| MultiPolygon M | 2006 |
| GeometryCollection M | 2007 |
| CircularString M | 2008 |
| CompoundCurve M | 2009 |
| CurvePolygon M | 2010 |
| MultiCurve M | 2011 |
| MultiSurface M | 2012 |
| Curve M | 2013 |
| Surface M | 2014 |
| PolyhedralSurface M | 2015 |
| TIN M | 2016 |
| Type | Code |
| Geometry ZM | 3000 |
| Point ZM | 3001 |
| LineString ZM | 3002 |
| Polygon ZM | 3003 |
| MultiPoint ZM | 3004 |
| MultiLineString ZM | 3005 |
| MultiPolygon ZM | 3006 |
| GeometryCollection ZM | 3007 |
| CircularString ZM | 3008 |
| CompoundCurve ZM | 3009 |
| CurvePolygon ZM | 3010 |
| MultiCurve ZM | 3011 |
| MultiSurface ZM | 3012 |
| Curve ZM | 3013 |
| Surface ZM | 3014 |
| PolyhedralSurface ZM | 3015 |
| TIN ZM | 3016 |
Implications
The extact list of FDO Providers that will be updated to support the new Geometry types has yet to be determined. This update process will most likely be done piecemiel, with the FDO API and SQLite support being implemented first, and changes to other providers made in subsequent releases. Implementation and support in multiple providers will depend greatly on available financing and developer resourcing.
The FDO Expression Engine will need to provide support for these new types. Functions such as SpatialExtents, Length2D, Area2D, etc.
Test Plan
The FDO API unit tests will be implemented to test basic FDO API changes.
All providers who implement support for these new Geometric Interfaces will be required to update their unit tests.
Funding/Resources
TBD
Attachments (1)
- geometryoverview.png (141.5 KB ) - added by 14 years ago.
Download all attachments as: .zip