About the new 3D distance functions in PostGIS 2.0.0

This is a presentation of the thoughts and logic behind the new 3D distance functions in PostGIS.
Please read it and don't hesitate to make some noise on the e-mail lists if something looks strange.

First some notes about the difference between 2D and 3D distance calculations:

After all it, all boils down to using Pythagoras theorem on two points to get the distance.

Pythagoras theorem works on three dimensions too. The problem is to find the two points…

In 2D the two closest points that we are seeking is always:

One vertexpoint on geometry 1 and one geometry on geometry 2
Example:

LINESTRING(1 1, 1 10) - LINESTRING(1 12, 1 14)

or

One vertex point on geometry 1 and a point somewhere along an edge on geometry 2 (or of course vice verse according to geometry 1 and 2)
Example:

LINESTRING(2 5, 10 5) - LINESTRING(1 1, 1 10)

What we also need to check is intersection edge to edge

In 3D there is a third possibility:
Both the points we are looking for (the two closest points on the geometries) might be on the edges.
Example:

LINESTRING(1 1 5, 10 1 5) LINESTRING(5 2 1, 5 2 10)

So, what we need to check for the different geometry types is:

Point – Point

Just Pythagoras theorem on the two points.
Example:

point(1 1 1) - point(2 2 2)

Point-Line

point-point calculation between the point and every vertex in the linestring
Example: see point-point above

point-edge calculation between the point and every edge in the linestring
Example:

point(5 5 5) - line(1 1 0, 1 10 0)

Point-Polygon

point-point calculation between the point and every vertex in the polygon
Example: see point-point above

point-edge calculation between the point and every edge in the polygon
Example: see point-edge above

point-surface calculation between the point and the surface of the polygon
Example:

point(5 5 10) polygon((1 1 1, 1 10 1, 10 10 1, 10 1 1, 1 1 1))

Line-Line

point-point calculation between every vertex in line 1 to every vertex in line 2
Example: see point-point above

point-edge calculation between every vertex point to every edge in the other geoemtry.
Example: see point-line above

edge-edge calculation between every edge in line 1 to every edge in line 2
Example:

line(1 1 5, 10 1 5) line(5 2 1, 5 2 10)

Line-Polygon

point-point calculation between every vertex in the line to every vertex in the polygon
Example: see point-point above

point-edge calculation between every vertex in the line to every edge in the boundary of the polygon and vice verse.
Example: see point-line above

edge-edge calculation between every edge in the line to every edge in the boundary of the polygon
Example: see line-line above

point-surface calculations between every vertex in the linestring to the surface of the polygon
Example: see point-polygon above

Polygon-Polygon

Actually polygon-polygon is the same calculations as line-polygon.
The two surfaces can not be closer to each other than any of the other options.
This is the equivalence in 3d to the not needed edge-edge calculation in 2d.

This is not the whole truth since one of the combinations here also needs a specific test to see if there is an intersection.

That is the case of edge-surface intersection.
Example:

line(5 5 0, 5 5 10) polygon((1 1 1, 1 10 1, 10 10 1, 10 1 1, 1 1 1))

In the other cases we can find the intersections by checking if the distance is 0

Defining the plane for surface calculations

One of the key parts of the 3D distance calculations is in calculations involving surfaces.
To do those calculations we need all points in a surface to be coplanar and we need to define this plane.

A plane can be represented in many ways.

• 3 points on the plane gives a definition of the plane
• 2 vectors can define a plane.
• 1 point on the plane and 1 vector perpendicular to the plane

There we use the third option

If our surface is a triangle like

POLYGON((1 1 1, 1 5 1, 9 3 2, 1 1 1))

then there is no problem.
The three unique points defines the plane and can not be anything else than coplanar.

But if there is more than 3 vertexes we can not be sure that they are coplanar.
Or more right, in most cases we can be sure that they are not coplanar because of precision problems.

So, how to handle this?

Here I will describe how this is done now in the distance calculations.
This is probably the part to most critical about.

There is no attempt to find if the points is not coplanar, just an attempt to get an approximation between the points if they are not perfectly coplanar.

Judging them as “not coplanar enough” should be a job for ST_IsValid instead since it will take to much power to do that on every distance calculation.

Ok, here is how the plane definition is done now:

First we find the average point of the surface by just adding all x-values, dividing with the number of vertexpoints and do the same for y and z.

This average-point should be on the plane and is the “point on the plane” in our plane definition.

Now we just need a perpendicular vector.

That we can get from any two points in the boundary of the surface together with our newly defined “point on the plane”.

If we take two points on the boundary of the surface and define lines between our point on plane and each of those, then we seek the line that is perpendicular to both this lines.

The most robust calculation we get if the line from our “point on plane” to the first point in the boundary is perpendicular to the second point on the boundary.
Since we don't know how the points are distributed along the boundary we have to do some assumptions.
We will also do the calculation about 4 times (3-5) and use the average answer.

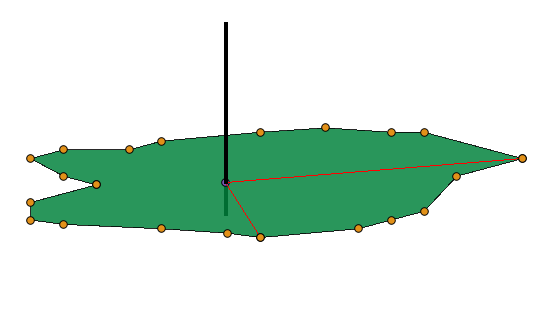
Lets say that we are trying to define the plane of a surface with 22 vertex points. We divide the surface in slices with ¼ of the vertex points in each slice. So in our example each slice contains 5 vertex-points.

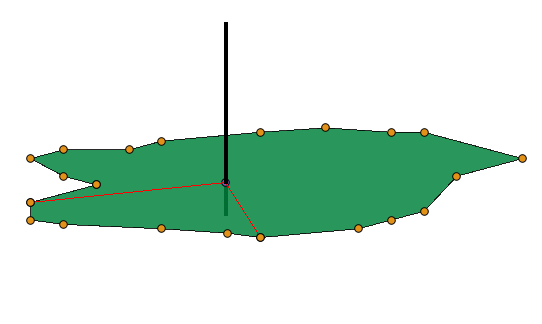
Then we use the first vertex point together with the 6:th and the “point on plane” to define a perpendicular line (vector actually) to the plane.

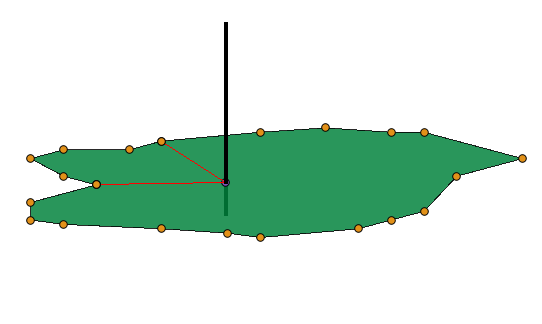
Then we use the 6:th vertex point and the 11 and do the same.

Then the 11 and the 16

and at last 16 and the 21.

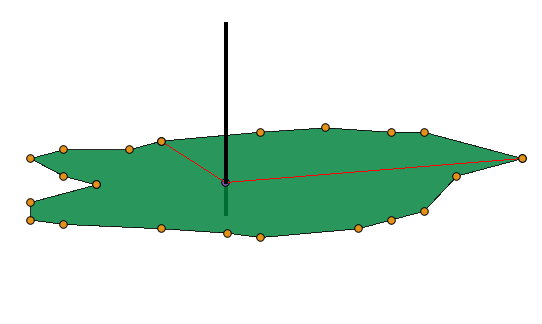
From those perpendicular vectors we calculate an average normal vector that we use in the surface calculations.

Depending on if the total number of vertex points is dividable by 4 the outcome will vary.

The idea is to walk the way around in about 4 steps and use the average result.

The code doing this can be found in http://trac.osgeo.org/postgis/browser/trunk/liblwgeom/measures3d.c

/Nicklas